Continuing the discussion from last month about applying integral control to electrohydraulic servosystems, we now shall focus on reducing the effects of disturbances that act upon control systems. The effects of these disturbances can be measured. Therefore, they can be corrected — within limits.
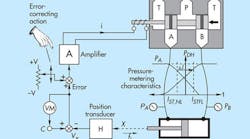
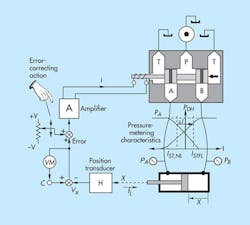
The system shown in Figure 1 is the same one that appears in Figure 1 from last month, but a human observer armed with an error-correcting potentiometer and voltmeter has been added. Consider that when there was no load on the cylinder, the system was at null; that is, the error-reading voltmeter would indicate zero. This can be done in a real system by adjusting the null control on a servovalve while observing the voltmeter (labeled VM) and continuing to adjust until the voltmeter reads zero.
Next, imagine that the magnitude of the load increases. For reasons already explained, the cylinder moves to a new position, resulting in a load-induced positioning error. But, more importantly, a readable voltage appears on the voltmeter. That value, divided by the position transducer gain (labeled H), is the amount of the position error.
Human-error correction
If the human observer turns the error-correcting pot while watching the voltmeter, and continues adjusting until it reads zero, the cylinder must go back to its original unloaded position. The load-induced error has been corrected! And if this is done at every stopping point, and sufficient time exists, all disturbances can be compensated for. This is the essence of integral control, but this example used a human operator affecting the control. Humans are good at such things. For example, in controlling the speed of a car, if the driver notices that speed is too low or too high, he or she increases or decreases power to the engine until the desired speed is achieved. Without thinking, the driver eliminates the error and, thus, performs the integral function.
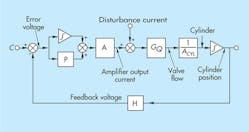
Putting a human being in every servoloop is not practical, so the solution to the disturbance problem is to implement integral control with hardware. This is easily accomplished with modern electronic devices; the concept is illustrated in Figure 2. Analog integration is done with an operational amplifier and with software in a digital controller.
What it means to integrate
The output of an integrator remains at its last value only if the input is exactly equal to zero. This means that the output increases or decreases — depending on the algebraic sign of the input — any time the input is not zero. If we apply this principle to the circuit at hand, we can easily see how the integrator performs the desired function of eliminating the disturbance error and, therefore, the following error.
Assume that command profile, C, in Figure 2 is sitting at a dwell level, and the cylinder is not moving. This means velocity must be zero. In other words, the input to the cylinder integrator must be absolutely zero. Now imagine that some sort of valve null disturbance causes the error voltage to become nonzero. That is, the command and feedback signals become unequal. With the controller integrator in place as shown, a nonzero input must change the integrator’s output. The increasing output is amplified and sent to the valve, which changes its opening, causing the cylinder to move. The question now is “How long will it move?” The answer lies in the input to the controller integrator. The system will not stop until both the velocity and the input to the controller amplifier become zero. Both integrators must have absolutely zero inputs to put the system in equilibrium (null).
However, neither output of the integrator has to be zero. In fact, the output of the controller integrator is what holds the valve spool at its disturbed position in order for the cylinder to undergo a force balance. In the process, the controller integrator has accumulated the disturbance, and its output provides the offset needed to compensate for that disturbance.
When speed remains constant
Now consider the case of a profiled input command when the profile is in its constant-speed (constant-slope) region. We have seen that a proportionally controlled positional servo requires an error between command and feedback to hold the valve open enough to produce the commanded speed. But if the cylinder is presumed to be moving at the commanded speed, the input to the cylinder integrator is a nonzero value related to the speed of the cylinder. Valve flow also is nonzero, and the valve is open by a considerable amount. Valve current, therefore, must be nonzero. If, for the moment, we ignore the possibility of disturbance current, then the input to the servoamplifier likewise is nonzero.
Now consider that the command and feedback signals are not equal. This results in a nonzero error — a nonzero input to the controller integrator. Under this condition, output of the controller integrator must be changing. In fact, if the feedback voltage lags behind the command voltage, then the controller integrator output must be increasing. This will increase the valve opening and cause the cylinder speed to increase. Thus, because some acceleration exists, we see that our earlier assumption of a constant output speed was in conflict with the nonzero error voltage.
Eliminating following error
The next question we pose is, “How long will the acceleration take place?” Again, the answer lies in examining the input and output of the controller integrator. The integrator output will continue increasing as long as a nonzero input signal exists. This means the system will be in a steady-state velocity condition only when the controller integrator input is zero, carrying further the requirement that the command and feedback voltages be exactly equal. In other words, the following error has been perfectly compensated! Not only have we compensated for effects of disturbances, we have also eliminated following error.
In the well-designed, integrally controlled servomechanism, the final output accuracy can approach that of the transducer alone. This is because the servoloop now contributes nothing to the error. Some people may claim that only the transducer limits the final accuracy. This position seems to be an overly optimistic conclusion and is subject to interpretation.