Hydraulic fluids perform four basic functions. Their primary function is to create force and motion as flow is converted to pressure near the point of use. Second, by occupying the space between metal surfaces, the fluid forms a seal, which provides a pressure barrier and helps exclude contaminants. A third function - often misunderstood - is lubrication of metal surfaces. The fourth and final function provided by hydraulic fluid is cooling of system components.
If any one of these functions is impaired, the hydraulic system will not perform as designed. Worse yet, sudden and catastrophic failure is possible. The resulting downtime can easily cost a large manufacturing plant thousands of dollars an hour. Hydraulic-fluid maintenance helps prevent or reduce unplanned downtime. It is accomplished through a continuous program to minimize and remove contaminants.
Aside from human interference, the most common source of system impairment is fluid contamination. Contamination can exist as solid particles, water, air, or reactive chemicals. All impair fluid functions in one way or another.
Sources of contaminants
Contaminants enter a hydraulic system in a variety of ways. They may be:
· built-in during manufacturing and assembly processes
·internally generated during normal operation, and
·ingested from outside the system during normal operation.
If not properly flushed out, contaminants from manufacturing and assembly will be left in the system. These contaminants include dust, welding slag, rubber particles from hoses and seals, sand from castings, and metal debris from machined components. Also, when fluid is initially added to the system, a certain amount of contamination probably comes with it. Typically, this contamination includes various kinds of dust particles and water.
During system operation, dust also enters through breather caps, imperfect seals, and any other openings. System operation also generates internal contamination. This occurs as component wear debris and chemical byproducts from fluid and additive breakdown due to heat or chemical reactions. Such materials then react with component surfaces to create even more contaminants.
Contaminant interference
In broad terms, contaminant interference manifests itself as either mechanical or chemical interaction with components, fluid, or fluid additives.
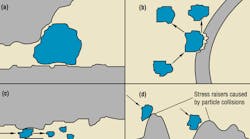
Mechanical interactions, Figure 1, include blockage of passages by hard or soft solid particles, and wear between particles and component surfaces.
Chemical reactions include: formation of rust or other oxidation, conversion of the fluid into unwanted compounds, depletion of additives - sometimes involving harmful byproducts - and production of biochemicals by microbes in the fluid.
Any of these interactions will be harmful. Without preventive measures and fluid conditioning, their negative effects can escalate to the point of component failure. One of the most common failure modes is excessive wear due to loss of lubrication.
Lubrication and wear
The pressures required in modern hydraulic systems demand sturdy, precisely matched components. And precision machining leaves very small clearances between moving parts. For example, it is not uncommon for control valves to have pistons and bores matched and fitted within a mechanical tolerance of ±0.0002 in. (two ten-thousandths of an inch). In metric units, this is about 5 µm (five millionths of a meter). In modern electrohydraulic devices, tolerances may be even tighter and clearances can be less than 1 mm. The surface finishes on high-pressure bearings and gears can result in rolling clearances as small as 0.1 µin.
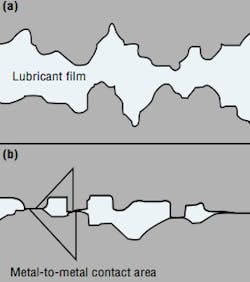
The hydraulic fluid is expected to create a lubricating film to keep these precision parts separated. Ideally, the film is thick enough to completely fill the clearance between moving parts, Figure 2. This condition is known as hydrodynamic or full-film lubrication and results in low wear rates. When the wear rate is kept low enough, a component is likely to reach its intended service-life expectancy - which may be millions of pressurization cycles.
The actual thickness of a lubricating film depends on fluid viscosity, applied load, and the relative speed of the two dynamic surfaces. In many applications, mechanical loads are so high that they squeeze the lubricant into a very thin film, less than 1-µin. thick. This is elastohydrodynamic (EHD) or thin-film lubrication. If loads become high enough, the film will be punctured by the asperities of the two moving parts. The result is boundary lubrication.
Component and system designers try to avoid boundary lubrication by making sure that fluid has the proper viscosity. However, viscosity changes as the fluid temperature changes. Also, loads and speed may vary widely during normal operating cycles. Therefore, most hydraulic components operate at least part of the time with only boundary lubrication. When that happens, parts of moving surfaces contact each other and are torn away from the parent material. The resulting particles then enter the fluid stream and travel throughout the system. If not removed by filtration, they react with other metal parts to create even more wear.
Fluid chemists continually try to minimize potential lubrication problems by improving fluids with additives. Viscosity-index (VI) improvers are added to help keep viscosity stable as temperature changes. Antiwear additives increase film strength. If very heavy loads will be applied, the fluid should contain an extreme pressure (EP) additive that reacts with metal surfaces to form a hard protective film. For fluids in circulating systems, defoamant, demulsifier, detergent, or dispersant may be added. Rust and oxidation (RO) inhibitors are used in most hydraulic fluids because air and water are always present to some extent.
Particle-generated wear
The symptoms of wear are diminished system performance and shorter component life. In pumps, wear may first be detected as reduced flow rate. This is because abrasive wear has increased internal clearance dimensions. Sometimes called increased slippage, this condition means that the pump is less efficient than it was when new. When pump flow rate decreases, the fluid system may become sluggish, as evidenced by hydraulic actuators moving slower. Pressure at some locations in the system also may decrease. Eventually, there can be a sudden catastrophic failure of the pump. In extreme cases, this can occur within a few minutes after initial start-up of the system.
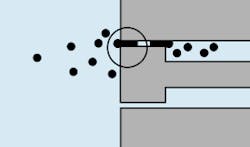
In valves, wear increases internal leakage. The effect this leakage has on the system depends on the type of valve. For example, in valves used to control flow, increased leakage usually means increased flow. In valves designed to control pressure, increased leakage may reduce the circuit pressure set by the valve. Silting interference, Figure 3, causes valves and variable-flow pump parts to become sticky and operate erratically. Erratic operation shows up as flow and pressure surges, causing jerky motion in actuators.
Water contamination of liquids
Water in oil-base fluids can be just as destructive as particle contaminants. And water exclusion is very difficult to accomplish. Because of its affinity for other liquids, water is present in some concentration in most hydraulic systems. The hygroscopic nature of liquids causes them to pick up a certain amount of water simply from contact with humid air. When condensation occurs in a reservoir, with subsequent mixing into the base liquid, more water can be added to the system. Water can even enter with new oil. An oil barrel stored outdoors in a vertical position is likely to have rainwater collect around its bung. With changes in ambient temperature, some of this moisture can be sucked into the barrel. Eventually, this water enters the system when the reservoir is filled from that barrel.
Besides these natural phenomena, there are several system- and maintenance-related sources of water. In machine tool applications, a good deal of water-base coolant can enter hydraulic systems through breather caps and imperfect seals. Worn and damaged heat exchangers can allow cooling water to leak through seals and ruptured lines into the oil system - and vice versa.
Each fluid has its own saturation level for water. Below the saturation level, water will be completely dissolved in the other fluid. For oil-base hydraulic fluids, the saturation level is likely to be in the range of 100 to 1,000 parts per million (0.01% to 0.1%) at room temperature. At higher temperatures, the saturation level is greater.
Above the saturation level, water becomes entrained, meaning that it takes the form of relatively large droplets. This also is called free water. Sometimes these droplets combine and precipitate to the bottom of the reservoir. At other times, due to churning or other mixing action, undissolved water is emulsified so that it exists as very fine droplets suspended in the oil.
Water's mechanical effects
When water concentration in hydraulic oil reaches 1% or 2%, the response of a hydraulic system may be affected. If water alters the hydraulic fluid's viscosity, the operating characteristics of the hydraulic system change. When the rate of water influx is swift, poor system response could be the first indication that water is present.
Cavitation is another symptom of water in the fluid. Because the vapor pressure of water is higher than hydrocarbon liquids, even small amounts of water in solution can cause cavitation in pumps and other components. This occurs when water vaporizes in the low pressure areas of components, such as the suction side of a pump. Vaporization is followed by the subsequent violent collapse of vapor bubbles against metal surfaces in these areas. The loud characteristic sounds of cavitation may be noticeable when this happens. The result is cavitation damage on the interior surfaces of hydraulic components because the metal has fatigued.
Emulsified water in oil
Tiny water droplets may be emulsified or suspended in oil-base fluids. Evidence of this is when the fluid appears cloudy or milky. Sometimes an oil/water emulsion is so tight that it is very difficult to separate the two fluids - even with the addition of a coalescing agent formulated to do this. While this is desirable in emulsion-type hydraulic fluids, it is highly undesirable for ordinary oil-base fluids. Some fluid additives encourage emulsification, while others (demulsifiers) discourage it. The viscosity of a water emulsion can be much different from its original base liquid. As noted earlier, lower viscosity reduces the thickness of lubricating films, leading to increased wear of surfaces in dynamic contact.
If free water is present in hydraulic fluid and the system operates at temperatures below 32° F, ice crystals may form. These crystals can plug component orifices and clearance spaces. In hydraulic systems, this will cause slow or erratic response.
Without fluid analysis to warn of water's presence and appropriate control measures, water content probably will increase to the point where these and other symptoms appear. Other symptoms include evidence of chemical-reaction products and eventually, component failures.
Chemical reactions due to water
Water reacts with almost everything in a hydraulic system. Water promotes corrosion through galvanic action by acting as an electrolyte to conduct electricity between dissimilar materials. The most obvious sign is rust and other oxidation that appears on metal surfaces. The inside top surface of the reservoir often is the first place rust becomes visible, but such rust still may go undetected unless the reservoir is drained and opened for servicing. Also, the time it takes for rust to form depends partly on the original surface treatment used to protect the metal used to build the reservoir.
Unfortunately, before rust is noticed in the reservoir, water probably has damaged other system components. An inspection of failed bearings and other components may point to corrosion damage. Corroded aluminum and zinc alloys could have a whitish oxide film. Steel bearing and gear surfaces may show signs of rust and pitting.
Water's reaction with oxidation inhibitors produces acids and precipitates. These water-reaction products also increase wear and interference. At high operating temperature (above 140° F), water reacts with and actually can destroy zinc-type antiwear additives. For example, zinc dithiophosphate (ZDTP) is a popular boundary lubricant added to hydraulic fluid to reduce wear in high-pressure pumps, gears, and bearings. When this type of additive is depleted by its reaction with water, abrasive wear will accelerate rapidly. The depletion shows up as premature component failure, resulting from metal fatigue and other wear mechanisms.
Water frequently can act as an adhesive that causes smaller contaminant particles to clump together in a larger mass. These gluey masses may slow down a valve spool, or cause it to stick in one position. Or these clumps could plug component orifices. In any case, the result is erratic operation or a complete system failure.
Microbial growth
Over time, water contamination can lead to the growth of microbes - minute life forms such bacteria, algae, yeasts, and fungi - in the hydraulic system. And the presence of air exacerbates the problem. Microbes range in size from approximately 0.2 to 2.0 µm for single cells, and up to 200 µm for cell colonies. Left unchecked, microbes can destroy hydraulic systems just as they destroy living organisms. Under favorable conditions, bacteria can reproduce (doubling themselves) as rapidly as every 20 minutes. Such exponential growth can form an interwoven mat-like structure that requires significant shear force to break up. This resistance quickly renders a fluid system inoperable. Besides their mass volume, bacteria produce acids and other waste products which attack most metals. When this happens, fluid system performance is degraded, and components fail more rapidly.
Evidence of microbial contamination
The first indication of microbial contamination may be the foul odor that comes from waste and decomposition products of the microbes. Fluid viscosity may increase due to the mass of material produced by these organisms. At the same time, the fluid may have a brown mayonnaise-like appearance, or slimy green look.
Unfortunately, by the time these symptoms appear, system components and the fluid itself may be severely damaged. This could require a major overhaul or replacement of the system.
Properly selected filters will remove microbes. But without adding biocides (substances capable of destroying these living organisms) to the fluid, fast-growing microbes can place a heavy load on system filters. Combined with wear debris and chemical reaction products, microbial contamination can result in rapid plugging of filter elements, requiring frequent replacement.
Water and air are essential for microbe growth. Eliminating water and air from a fluid minimizes microbial problems. But some systems use water as the base fluid, and air is very difficult to exclude from fluids in operating hydraulic systems. With water and air present, microbes can usually find some fluid component to feed their growth. When water can not be controlled by exclusion or removal, biocides should be added to the fluid. A biocide combined with properly selected water-absorption filters can help minimize chemical-reaction byproducts and microbial contamination.
Exclusion practices
The first defense against fluid contaminants is preventing their entry into a hydraulic system. After that, removing contaminants before system start-up prevents much damage that can occur early in a system's life. Thereafter, well-planned routine maintenance will maintain the fluid in peak condition. Here are some of the initial positive steps that can be taken:
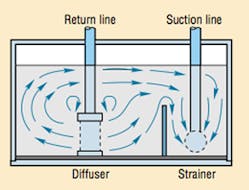
- fit the reservoir with baffles and return-line diffusers, Figure 5, to prevent churning that whips air into the fluid
- equip the reservoir with a breather having an air-filter element with a rating of at least 99% efficiency at 2 µm
- make sure all fittings are properly tightened (besides causing leakage, loose fittings can allow airborne dust to be sucked into the system)
- flush the system thoroughly before it goes into service
- prefilter fluid before filling the reservoir (it should be as clean as your specification for the system fluid)
- inspect filter indicators to make sure they are working
- use boots and bellows to protect cylinder rods and seals
- replace filter elements before the filter bypass valve opens; otherwise, the system will operate with no filtration
- replace any worn seals and hoses promptly; if not done, the negative effects are the same as loose fittings
- practice good housekeeping whenever a system is opened for maintenance; protect replacement components from contamination, and
- analyze fluid regularly to detect problems such as overheating, leaking water, clogged heat exchangers, additive breakdown, etc.
Removal mechanisms
Once contamination is in the fluid, it may be reduced and controlled by settling, outgassing (e.g. in aerated liquids), filtration/separation, and fluid replacement. The first two mechanisms - settling and outgassing - occur naturally, but their effect can be enhanced by controlling the fluid environment through system design. The latter two also require human involvement, again during system design or in maintenance activities after installation.
For settling to occur, a contaminant must have a density greater than the fluid transporting it. The lower the density of a contaminant particle, the more buoyant it will be in the fluid. The flow rate of the fluid also helps determine how quickly a contaminant will settle. A contaminant transported by a fluid will stay in suspension if the flow velocity supplies enough lifting force to overcome gravity. If flow is turbulent, it is more likely that contaminants will stay in suspension.
As mentioned previously, the reservoir can be designed with baffles and return-line diffusers to reduce fluid velocity enough so that larger particles will settle. On the other hand, contaminants must remain in suspension if they are to be transported to a filter for removal. This is particularly important in fluid lines and components, where particle settling can cause unpredictable contaminant removal rates, or silting interference between moving parts. Therefore, system designers want a reasonable degree of turbulence in the hydraulic system so that smaller particles remain in suspension. This is as true for the reservoir as elsewhere in the system. A tapered reservoir bottom will help prevent the collection of smaller contaminant particles due to its reduced bottom surface area and tendency to extend the turbulence effect. As in many design projects, reservoir construction and piping configuration involves compromises.
Outgassing can be thought of as the inverse of settling. If fluid turbulence is low enough to prevent mixing action, dissolved air can come out of suspension and rise to the surface of a liquid. Whether the air actually leaves the liquid or not depends on the relative surface tensions and partial pressures of the air and the liquid. The lower the turbulence in the reservoir, the more likely it is that a contaminant will leave the fluid by way of outgassing or settling.
Natural mechanisms, such as settling and outgassing, cannot by themselves reduce contamination to an acceptable level. In the absence of filtration and separation devices, the only alternative is to replace the fluid at periodic intervals. Even with adequate filtration, fluid replacement cannot be postponed forever. This certainly is true for automotive lubricants, and points out a fundamental fact of fluid life. There is an economic trade-off between the cost of buying, installing, and servicing filters and separators, and the cost of replacing the hydraulic fluid more often.
Fluid conditioning objectives
The objective of hydraulic fluid conditioning is to lower total operating costs. If the system can meet or exceed minimum standards for fluid cleanliness, one or more of these intermediate goals can be achieved:
- reduce maintenance requirements for the fluid system and components
- improve the performance of the system and its fluid
- assure the quality of the final product by improving machine operation, and
- enhance safety and/or reduce risk of injury to personnel (for example, by eliminating the need for maintenance on or around operating equipment).
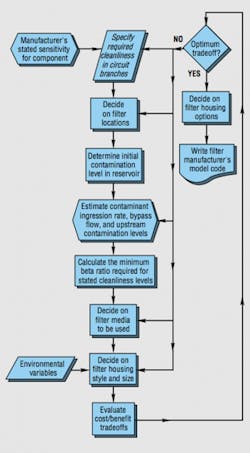
Appropriate fluid conditioning increases the mean time between hydraulic component failures. Still, this benefit has to be properly balanced against the cost of purchasing the filters, replacing elements, and maintaining filtration equipment. Careful filtration system design and component selection will help minimize these costs. The best way to optimize the benefit/cost trade-off is to follow sound practices for the selection of filters, elements, and filter media. One general process is illustrated in the filter-specification flow chart, Figure 5.
Many questions should be answered regarding contaminant removal:
- how clean does the fluid be have to?
- what size particles must be removed?
- how many particles within a given size range need to be removed?
- how efficient must the filter media be in terms of the percentage removal of a given size range - and in terms of dirt-holding capacity?
- will the fluid contamination stabilize at an acceptable level for a given combination of filters and media?
Component sensitivity
As the flow chart implies, specifiers need to have a feel for the sensitivity of hydraulic components to contaminants of various sizes and concentrations. Designers and users have observed that some components are more sensitive to contaminants than others. For example, they may have seen a certain pump quickly fail, while another type lasts for months in the same system. They also probably have noticed that higher pressures and flow rates tend to make all components wear out more quickly. Those who are particularly observant may have noticed that the higher the concentration of airborne contaminants around systems, the sooner they fail. These factors combine to influence the service life of components.
Another point is that filter media with small pore sizes frequently are more costly, and must be replaced more often than coarser media. For practical economic reasons, designers must find a compromise between costly ultrafine filtration and the cost of early component failures. This compromise is to have fluid only as clean as it needs to be, not as clean as possible.
Designers tend to rely on their own experience as well as information from component manufacturers to determine how clean hydraulic fluid needs to be. Some conservative manufacturers assume that worst-case conditions exist and specify a very low acceptable level of contamination for their components. Others take a middle-of-the-road approach, and specify cleanliness for more or less average conditions.
Additional sources
Manufacturers' recommendations can be augmented by information that is available from other sources. For example, OEMs and research laboratories have carried out projects to analyze the sensitivity of pumps, valves, and other components to contaminants. As a result, guidelines and standards for hydraulic-fluid cleanliness have been published. These guidelines attempt to interrelate diverse factors such as:
- fluid lubricity (e.g., water-base fluids have lower lubricity than oil)
- abrasiveness of the contaminants commonly found in hydraulic systems
- system duty cycle and cycle rate (high pressure and high cycle rates, combined with contaminants, lead to earlier fatigue failures)
- component replacement cost
- design life objective in terms of mean time before failure (MTBF); a common goal today is 10,000 hours or more, and
- degree of risk associated with contaminant-related failures (high risk of personal injury or high cost of lost production dictates a need for cleaner fluid.)
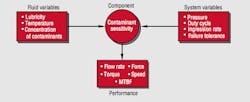
Fluid variables and system variables both have an effect on a component's sensitivity to contamination. This sensitivity eventually is reflected in system performance, Figure 6.
The International Standards Organization (ISO) recommends cleanliness levels for various types of components, see the table below. The levels are stated in terms of industry standards that have been recognized for the past 20 years. Many fluid power designers apply these recommendations as rules of thumb. Many specifiers now accept and use ISO 4406 (see table on page A/99) as a means of designating the fluid cleanliness required for their systems.
Importance of records
Still, component manufacturers' and industry guidelines should be modified by experience. That requires gathering enough operating and maintenance data over sufficient time and from enough systems to provide confidence to make decisions. The data gathered should include the results of regular fluid analysis on systems. The categories of data collected might include:
Fluid variables - flow, pressure, temperature, and viscosity for circuit branches with the most sensitive or expensive components.
Fluid analysis - particle counts in various size ranges (e.g., >2, >5, >15, >25, >50, and >100 µm), spectrochemical analysis (e.g., most likely metals and other contaminants), and water content (% by volume).
Filtration information - model number and manufacturer for the filter(s) and element(s) protecting the circuit for which other data was gathered; element performance ratings in terms of beta ratios and dirt-holding capacity.
Maintenance data - date system placed in service; dates and descriptions of routine maintenance performed (including element replacements); reading of the filter element condition indicator (e.g., "needs replacement" or "in bypass"); dates and descriptions of component failures, including manufacturers' names and model numbers; failure mode analysis (e.g., fracture, corrosion, wear, etc.) also would be very helpful in determining if contamination was a factor in any failures.
PC data base and statistical analysis programs also can be used to correlate failures with fluid contamination levels. This will create a picture of the contamination tolerance of the most sensitive components. It also allows for the calculation of MTBFs for specific components, certain circuit branches, or the system as a whole.
Obviously, this is data the user must collect. Still, manufacturers can monitor warranty claims as an opportunity to capture some of this data, and create a clearer picture of component sensitivity. That may cover only the first year or two of service. A close relationship with customers and distributors can provide an opportunity to gather similar data over longer periods of time as replacement parts are ordered.
Descriptive factors for particlesParticulate contamination may be characterized by the following identification factors. agglomeration the tendency of particles to bond together. This action is generally detrimental in fluid-contamination control. compaction degree of packing from sedimentation process. As void spaces decrease and bulk density increases, silt condition intensifies. concentration weight per unit volume of fluid or number of particles greater than given size per unit volume of fluid. density mass of particle per unit of volume. Density affects the rate at which particles settle out from the fluid. dispersion the tendency of particles to remain separated. This is a factor in particle separation and analysis. hardness resistance to abrasion and the particles potential to abrade exposed surfaces. settling terminal velocity of particles controls the degree of particle suspension provided by the flowing fluid. shape degree of irregularity of particle structure or topography. A factor important to the cutting or abrading ability of the particle. size structural extent of particle as defined by geometric, derived, and hydrodynamic diameters. Such diameters have significance on a statistical basis. size distribution frequency of occurrence of each particle size in the population. Cumulative particle size distribution curves are the most popular type in fluid-contamination control. size limits the size range in which only fractureless deformation occurs and the lower filtration limit of interest. state condition where size and shape cannot be altered without forceful shearing of crystalline or molecular bonds. A concept important to the understanding of particle generation and growth. transport the life force needed to overcome the buoyant weight of the particle. When this is achieved, the flow conduit does not retain particles on its surface. |
Contamination - dynamic, not static
Another reason for regular fluid analysis is that the contamination level changes with time, and varies by location in the system. At any point, the amount of contamination present in the fluid depends on three factors:
1. How contamination much was in the fluid when the system was started
2. How much was added to the fluid from all sources during operation (Ingression rate is the term used to describe the amount of contaminant entering the fluid per unit of time.)
3. How much contamination left the fluid due to all removal mechanisms (settling, and filtration or separation)
These three factors account for the total mass of contaminant in a system at any time. That mass can be calculated using a material-balance equation:
CT = Ct + Ca - Cs
where:
C is contaminant
T is any point in time
t is time since start of process
Ca is amount added since t
Cs is amount removed since t
The term material balance is used because the equation calculates the net difference between the amount of material or contaminant entering and leaving the fluid, and adds this difference to what was already there. The calculation applies to a specific location in the system.
In a circulating system, contaminants not removed will appear at the filter inlet again, along with new contaminant added to the fluid. This is called a multipass system because the fluid and contaminant make multiple passes through the filter. As a result, the contaminant concentration in the system fluctuates continuously.
If we consider the initial start-up of a system, the contaminants already present are there as a result of manufacturing processes or have entered with new fluid. (Each milliliter of fluid out of the original barrel typically contains at least 2,500 particles that are 5 mm and larger in diameter.) A few minutes after start-up, the particulate level will be considerably higher due to flushing action of the fluid as it flows through new components and piping to pick up debris. Eventually, more particles enter the system through the reservoir breather and imperfect seals. Still more will be added over time due to internal wear.
Fluid cleanliness required for typical hydraulic components
ISO code
Estimating ingression rate
Assume that a new hydraulic system has been flushed properly before being put into service. If the system has a multipass filtration system with a given flow rate, the eventual stabilized level of contaminants will depend on the system's ingression rate and filter media removal efficiency. If filter efficiency is too low, the contaminant level will continue to increase due to the wear particles generated within the system and new particles entering from outside the system. (This is the scenario in most automobile lubrication systems, and why motor oil should be changed periodically.) If filter efficiency is high enough, the contaminant level will decrease and become stabilized, extending the service life of the hydraulic fluid. Because operating conditions vary, this is a kind of dynamic stability. The contaminant level varies within a range determined by these conditions.
Therefore, to select the appropriate filter media, it is necessary to have some idea of the ingression rate. Of course the ingression rate probably varies at different locations in the system, and depends on these factors:
- concentration of ambient airborne contaminants (which enter through worn filler/breathers, loose fittings, leaking seals, etc.)
- use or absence of an air-filter element in the reservoir breather
- number of components in the system or circuit branch
- types of components that make up the system, particularly if there are rotating components such as pumps and motors (some types wear faster than others)
- fluid velocity (because higher velocity often may accelerate wear - after flushing is completed)
- system pressure (because higher pressure also tends to increase wear rates)
- fluid temperature (excessive heat can cause fluid and additives to break down, creating contamination), and
- the filter media used (more-efficient media results in lower contaminant levels and reduced wear rates).
This parade of factors makes accurate estimation of ingression rates difficult. An estimate can be made by conducting particle counts on fluid samples taken from a system with known operating conditions and filtration efficiency. (In multibranch circulating systems, the reservoir frequently is picked as a convenient location from which to take samples.) Then, by using a simple filtration model based on the material-balance equation, an ingression rate can be inferred. Filtration specifiers can construct their own estimates using the same technique. Such an estimate may be more accurate than one of the averages published in a table. Computerized filtration models also are available that allow a large number of variables to be quickly manipulated in a kind of ingression-rate What if? analysis.
Cleanliness reference
In order to detect or correct problems, a contamination reference scale is used. Particle counting is the most common method to derive cleanliness level standards. Very sensitive optical instruments count the number of particles in various size ranges in a fluid sample. These counts are reported as the number of particles greater than a certain size found in a specified volume.
The ISO 4406 cleanliness level standard has gained wide acceptance in most industries today. A modified version of this standard references the number of particles greater than 2, 5, and 15 micrometers in a known volume - usually 1 milliliter or 100 milliliters. (The number of smaller-size particles helps predict silting problems. A high number of larger particles might indicate catastrophic component failure.)
ISO 4406 range numbers
number
Filter media
The filter media is that part of the element which actually contacts contaminant and captures it for subsequent removal. The nature of the particular filter media and the contaminant-loading process designed into the element explains why some elements last longer in service than others.
During manufacture, media usually starts out in sheet form, then is pleated to expose more surface area to the fluid flow. This reduces pressure differential across the element while increasing dirt-holding capacity. In some designs, the filter media may have multiple layers and mesh backing to achieve certain performance criteria. After being pleated and cut to the proper length, the two ends are fastened together using a special clip, adhesive, or other seaming arrangement to form a cylinder. The most common media include wire mesh, cellulose, and fiberglass composites, or other synthetic materials. Filter media is generally classified as either surface- or depth-type.
Surfacemedia — For surface-type filter media, the fluid stream basically flows in a straight path through the element. Contaminant is captured on the surface of the element which faces the fluid flow. Surface-type elements are generally made from woven-wire cloth. Because the process used to manufacture the wire cloth can be controlled very accurately, and the wire is relatively stiff, surface-type media have a consistent pore size. This consistent pore size is the diameter of the largest hard spherical particle that will pass through the media under specified test conditions. However, during use, the build-up of contaminant on the element surface will reduce the pore size and allow the media to capture particles smaller than the original pore-size rating. Conversely, particles (such as fiber strands) that have smaller diameters but greater length than the pore size may pass downstream through surface media.
Depth media — For depth-type filter media, fluid is forced to take convoluted indirect paths through the element. Because of its construction, depth-type media has many pores of various sizes formed by the media fibers. This maze of multi-sized openings throughout the material traps contaminant particles. Depending on the distribution of pore sizes, the media can have a very high capture rate for very small particle sizes.
General comparison of filter media
efficiency
holding
capacity
pressure
life
cost
The two basic media that are used for depth-type filter elements are cellulose (or paper) and fiberglass. The pores in cellulose media tend to have a broad range of sizes and are very irregular in shape due to the irregular size and shape of the fibers. In contrast, fiberglass media consist of man-made fibers that are very uniform in size and shape. These fibers are generally thinner than cellulose fibers, with a consistently circular cross-section. The differences between these typical fibers account for the performance advantage of fiberglass media. Thinner fibers can provide more pores in a given area. Furthermore, thinner fibers can be arranged closer together to produce smaller pores for finer filtration. Dirt-holding capacity, as well as filtration efficiency, are improved as a result.
Particle counting
Knowing the cleanliness level of the hydraulic fluid in a system is the basis for selecting contamination-control measures. Particle counting is the most common method of deriving cleanliness-level standards. Very sensitive optical instruments count the number of particles in various size ranges in a measured fluid sample. These counts are reported as the number of particles greater than a certain size found in a specified volume of fluid.
The ISO 4406 Cleanliness-Level Standard is accepted in most industries today. A widely used, modified version of this standard references the number of particles greater than 2, 5, and 15 µm in a known volume - usually 1 or 100 milliliters. The number of particles greater than 2 and 5 µm is a reference point for silt particles, those which can cause clogging problems. The 15-µm size range indicates the quantity of larger particles present, those which contribute greatly to possible catastrophic component failure.
To identify a cleanliness level, the number of particles in the sample for each of the three measured sizes is referred to the ISO 4406 chart, and given an appropriate range number. If a fluid sample contained between 1,300 and 2,500 2-µm and larger particles (range 18); between 320 and 640 5-µm and larger particles (range 16); and between 40 and 80 15-µm and larger particles (range 13); the sample would be classified as 18/16/13. Note that the numbers that make up the ISO cleanliness-code classification will almost never increase as the particle size increases.
Most manufacturers of hydraulic (and load-bearing) equipment conduct tests and then specify an optimum or target cleanliness level for their components. Exposing components to hydraulic fluid with higher than optimum contamination levels may shorten the component's service life. It always is best to consult with component manufacturers and obtain their written fluid-cleanliness-level recommendations. This information is needed in order to select the proper level of filtration. It also may prove useful for any subsequent warranty claims, as it may draw the line between normal operation and excessive or abusive operation.
The Multipass Test
The filtration industry uses the ISO 4572 Multipass Test Procedure (also recognized by ANSI and NFPA) to evaluate filter element performance. During the Multipass Test, Figure 7, fluid circulates through the test circuit under precisely controlled and monitored conditions. The differential pressure across the element being tested is continuously recorded, while a constant amount of contaminant is injected upstream of the element. On-line laser particle sensors measure the contaminant levels upstream and downstream from the test element. (Note that the results of this test are very dependent on flow rate, type of contaminant, and terminal pressure differential.)
The Multipass Test determines three important element-performance characteristics:
1. Dirt-holding capacity.
2. Pressure differential of the test filter element.
3. Separation or filtration efficiency, expressed as a beta ratio.
Beta ratio
The beta ratio (also known as the filtration ratio) is a measure of a filter element's particle-capture efficiency. Therefore, it is a performance rating. Here is how a Beta Ratio is derived from Multipass Test results. Assume that 50,000 particles, l0 µm and larger in size, were counted upstream from the test filter, and 10,000 particles in that same size range were counted downstream from the filter. Substituting in the equation:
βx = (NU)/(ND)
where: x is a specific particle size,
NU is the number of particles upstream, and
ND is the number of particles downstream.
Therefore, β10 = 50,000/10,000 = 5
This result would be read as "Beta ten equal to five." Now, a beta ratio number alone means very little. It is a preliminary step to finding a filter's particle-capture efficiency. This efficiency, expressed as a percent, can be found by a simple equation:
Efficiencyx = 100 (1 - 1/β)
Efficiency10= 100 (1 - 1/5) = 80%
In this example, the particular filter element tested was 80% efficient at removing 10-µm and larger particles. For every five particles in this size range introduced to the filter, four were trapped in the filter media.
capture efficiencies
(at a given
particle size)
(at the same
particle size)
Contaminant loading
The term contaminant loading in a filter element refers to the process of filling and blocking the pores throughout the element. As contaminant particles load the element's pores, fewer open paths remain for fluid flow, and the pressure required to maintain flow through the media increases. Initially, the differential pressure across the element increases slowly because plenty of open pores remain for fluid to pass through. The gradual pore-blocking process has little effect on overall pressure loss.
Eventually, however, successive blocking of media pores significantly reduces the number of pores open for flow. The differential pressure across the element then rises exponentially as the element nears its maximum life. As the element continues to load with contaminant, the pressure differential across the filter will continue to increase. This goes on until the bypass valve (if installed) opens, the element (if without bypass protection) fails structurally, or the clogged element is replaced. The quantity, size, shape, and arrangement of the pores throughout the element accounts for why some elements last longer than others.
Consider two of the most common filter media: cellulose and fiberglass, For a given media thickness and filtration rating, there are fewer pores in cellulose media than fiberglass. Accordingly, the contaminant-loading process would block the pores of the cellulose media element more quickly than an identical fiberglass media element.
Multi-layer fiberglass media elements are relatively unaffected by contaminant loading for a longer time. The upstream media has relatively larger pores to capture larger particles; the downstream media layer with very small pores captures the greater quantity of small particles present in the fluid.
Cleanliness required for typical hydraulic components
Filter-element life profile
Every filter element has a characteristic relationship between pressure differential and contaminant loading. This relationship can be defined as the filter element life profile. The actual life profile obviously is affected by the system operating conditions. Variations in the system flow rate and fluid viscosity affect the clean pressure differential across the filter element and have a well-defined effect upon the actual element life profile.
The filter element life profile is very difficult to evaluate in actual operating systems. The system's ratio of operating time to idle time, the duty cycle, and the changing ambient contaminant conditions all affect the life profile of the filter element. In addition, precise instrumentation for recording the change in the pressure loss across the filter element seldom is available. Most machinery users and designers simply specify filter housings with differential-pressure indicators to signal when the filter element should be changed.
Multipass test data can be used to develop the pressure-differential-versus-contaminant-loading relationship. As mentioned, operating conditions such as flow rate and fluid viscosity affect the life profile of a filter element. Life profile comparisons can be made only when all these operating conditions are identical, and the filter elements are the same size.
Under those conditions, the quantity, size, shape, and arrangement of the pores in the filter element determine the characteristic life profile. Filter elements manufactured from cellulose media, single-layer fiberglass media, and multi-layer fiberglass media have very different life profiles.
Filter housings
The filter housing is the pressure vessel which contains the filter element. It usually consists of two or more subassemblies, such as a cover (or head) and a removable bowl that allows access to the element. The housing has inlet and outlet ports that enable fluid to enter and leave. Housing options may include bypass valves and element-condition indicators.
Primary concerns in the housing-selection process include mounting methods, porting options, indicator options, and pressure rating. Except for the pressure rating, all depend on the physical system arrangement and the preferences of the system designer. Pressure rating of the housing is far less arbitrary; it is determined by system needs before the housing style is selected.
Pressure ratings
Location of the filter in the circuit is the primary determinant of pressure rating of the component. Filter housings are generically designed for one of three locations in a circuit: suction, pressure, or return lines. One characteristic of these locations is their maximum operating pressures. Suction and return line filters are generally designed for lower pressures - 500 psi or less. Pressure filter locations may require ratings from 1,500 to 6,000 psi.
Note that it is essential to analyze the circuit for pressure-spike potential as well as steady-state conditions. Some housings have restrictive or lower fatigue pressure ratings. In circuits with frequent high-pressure spikes, another type housing may be necessary to prevent fatigue-related failures.
Bypass valves
Bypass valves open flow paths around filter elements to prevent their collapse or bursting when they become heavily loaded with contaminant. As contaminant builds up in the element, the differential pressure across the element increases. At a pressure well below the failure point of the filter element, the bypass valve opens, allowing flow to go around the element. Some bypass valve designs have a bypass-to-tank option. This directs the unfiltered bypass flow back to the tank through a third port, preventing unfiltered bypass fluid from entering the system. Bypass valves also prevent pump cavitation when used with suction line filters. When specifying a bypass-type filter, it generally can be assumed that the manufacturer has designed the element to withstand the bypass valve differential pressure when the bypass valve opens.
Note that some of the upstream contaminant particles also bypass the filter element with the fluid and enter the downstream system. When this happens, the effectiveness of the filter element is compromised and the attainable system fluid cleanliness degrades.
Other filters are designed specifically with no bypass valve (sometimes called a blocked bypass). They prevent any unfiltered flow from going downstream, thus protecting servovalves and other contaminant-sensitive components. In filters without bypass valves, higher collapse-strength elements may be required, especially if installed in high-pressure locations. When specifying a non-bypass filter design, make sure that the element has a differential-pressure rating close to the maximum operating pressure of the system, and that the filter has a condition indicator.
After a housing style and pressure rating are selected, the bypass valve setting needs to be chosen. This setting must be established before sizing the filter housing. Everything else being equal, the highest bypass cracking pressure available from the manufacturer should be specified. This will provide the longest element life for a given filter size. Occasionally, a lower setting may be selected to help minimize energy loss in a system, or to reduce backpressure on another component. In suction filters, either a 2- or 3-psi bypass valve is used to minimize the chance of potential pump cavitation.
Element-condition indicators
The element-condition indicator signals when the element is loaded to the point that it should be cleaned or replaced. The indicator usually has calibration marks which also indicate if the bypass valve has opened. The indicator may be linked mechanically to the bypass valve, or it may be an entirely independent differential-pressure sensing device. Indicators may give visual or electrical signals or both. Generally, indicators are set to trip at a differential pressure anywhere from 5% to 25% below that which opens the bypass valve.
Sizing housing and element
The filter housing size should be large enough to achieve at least a 2:1 ratio between the bypass valve setting and the pressure differential of the filter with a clean element installed. For longer element life, this ratio should be 3:1 or even higher.
Referring to typical flow/differential-pressure curves from a manufacturer's catalog, the filter specifier needs to know the operating viscosity of the fluid and the maximum (not the average) flow rate to assure that the filter does not spend a high portion of time in bypass due to flow surges. This is particularly important in return-line filters, where flow multiplication from large cylinders may increase the return flow compared to the pump's flow rate.
Always consider ambient temperature conditions when sizing filters. Low ambient temperatures may increase fluid viscosity to the point where pressure differential across the filter assembly also may increase considerably.
If a filter was fitted with a 50-psi bypass valve, the initial (clean) pressure differential should be no greater than 25 psi and preferably 16 2/3 psi or less. These pressures are calculated from the 3:1 and 2:1 ratios of the 50-psi bypass setting and initial pressure differential.
Standard filter assemblies normally are manufactured with a bypass-valve cracking pressure between 25 and 100 psi. The bypass valve in most of these assemblies actually limits the maximum pressure drop across the filter element. As the element becomes blocked with contaminant, the pressure differential increases until it reaches the bypass valve cracking pressure. At this point, part of the flow through the filter assembly begins to bypass the element through the valve. This action limits the maximum pressure differential across the filter element.
The relationship between the starting clean pressure differential across the filter element and the bypass valve pressure setting must be considered. A cellulose element has a narrow region of exponential pressure rise. For this reason, the relationship between the starting clean pressure differential and the bypass valve pressure setting is very important. This relationship in effect determines the element's useful life.
In contrast, the useful element life of single-layer and multi-layer fiberglass elements is established by the nearly horizontal, linear region of relatively low pressure drop increase, not the region of exponential pressure rise. Accordingly, the filter assembly's bypass valve cracking pressure, whether 25 or 75 psi, has relatively little impact on the useful life of the element. Thus, the initial pressure differential and bypass valve setting is less a sizing factor for fiberglass media.
Filter types and locations
The type of filter - suction, return, pressure, or off-line - and its physical location in the circuit are almost inseparable by definition.
Suction filters serve to protect the pump from fluid contamination. They are located upstream from the pump's inlet port. Some may be simple inlet strainers, submersed in fluid in the tank. Others may be mounted externally. In either case, suction filters have relatively coarse elements, due to cavitation limitations of pumps. (Some pump manufactures do not recommend the use of a suction filter. Always consult the pump manufacturer for inlet restrictions.) For this reason, suction filters are not used as a system's primary protection against contamination, and in fact, the use of suction strainers and filters has greatly decreased in modern hydraulic equipment.
Return filters may be the best choice if the pump is particularly sensitive to contamination. In most systems, the return filter is the last component through which fluid passes before entering the reservoir. Therefore, it captures wear debris from all of the system's working components and any particles that enter through worn cylinder rod seals before such contaminant can enter the reservoir and be pumped back into the system. Because this filter is located immediately upstream from the reservoir, its pressure rating and cost can be relatively low.
Note that retracting some cylinders with large diameter rods may result in flow multiplication. This high return-line flow rate may open the filter bypass valve, allowing unfiltered fluid to pass downstream. This probably is an undesirable condition and should be considered when specifying the filter.
Pressure filters are located downstream from the system pump. They are designed to handle the system pressure and are sized for the specific flow rate in the pressure line where they are located. Pressure filters are especially suited for protecting sensitive components, such as servovalves, directly downstream from the filter. Because pressure filters are located just downstream from the pump, they also help protect the entire system from any pump-generated contamination.
Duplex filters, a common special configuration, may include both pressure and return filters. Duplex filters provide continuous filtration. They have two or more filter chambers and include the necessary valving to allow for uninterrupted operation. When one filter element needs to be serviced, the duplex valve is shifted, diverting flow to the opposite filter chamber. The dirty element can then be changed, while flow continues to pass through the cleaner element. The duplex valve typically is an open cross-over type, which prevents any flow blockage.
Off-line filtration is an increasingly popular filtration arrangement. Also referred to as recirculating, kidney loop, or auxiliary filtration, it operates independent of a machine's main hydraulic system. This makes it attractive as a retrofit project for problem systems. An off-line filtration circuit includes its own pump and electric motor, a filter, and the appropriate connecting hardware. These components are installed off-line as a small subsystem separate from the working lines, or they may be included in a fluid-cooling loop. Fluid is pumped continuously out of the reservoir, through the off-line filter, and back to the reservoir. A rule of thumb: the off-line pump should be sized to flow a minimum of 10% of the main reservoir volume.
With its polishing effect, off-line filtration is able to maintain the system's fluid at a constant contamination level. As with a return line filter, the off-line loop is best suited to maintain overall system cleanliness; it does not provide protection for specific components. An off-line filtration loop has the added advantage that it is relatively easy to retrofit on an existing system that has inadequate filtration. Also, the off-line filter can be serviced without shutting down the main system.