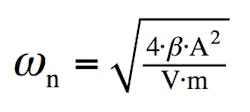Controlling electrohydraulic servo systems has always been just a little more challenging than controlling electromechanical servomotor systems. The main reason is that electrohydraulic systems use compressible oil to move the actuator. A hydraulic system can be thought of as a mass between two springs where the piston and the load is the mass, and the oil on both sides of the piston represents the two springs. Servomotor systems are simpler because, for the most part, only the inertia of the motor and the connected load must be considered.
Achieving design goals
For optimal design of a hydraulic system, the fastest response to disturbances and errors should be applied. However, to achieve this goal, you must either increase the damping factor or increase the natural frequency of the system. Adding friction will increase the damping factor. Another way to provide damping is to add a small orifice between the A and B ports of the valve. Unfortunately, both of these methods waste energy.
Increasing the diameter of the cylinder can increase its natural frequency, but that increases cost because a larger cylinder, valve, accumulator, and pump will be required. It is less expensive and more effective to use electronics to get around the limitations. To do this, the PID may be extended to include a second derivative gain, but hurdles must be overcome before a second derivative gain can be used.
Another enhancement is to use an electronic motion controller that can add a jerk feed-forward term to the control loop. Jerk is the derivative (rate of change) of acceleration. Feed forwards are estimates of what the control output should be to the valve to achieve a target velocity, acceleration, and jerk.
If the model for the actuator is known exactly, and no disturbances occur, then, theoretically, you could control a servohydraulic actuator perfectly without using closed-loop control. It should be obvious that the valve should be opened up proportionately to the target velocity, and a velocity feed forward can do that. Why wait for the PID to respond to an error?
The acceleration and jerk feed forwards work on the same principle, but take into account how the oil compresses as it applies force to the load. In practice, the model for the actuator is not known exactly and it isn’t perfectly linear, so closed loop control is still required. When set correctly, the feed forwards can estimate the control output usually to within 5% of the required control signal. Then, the PID needs only to provide a small correction to the control signal due to non-linearities and changes in load.
Challenges of second order control
Adding a second derivative gain and jerk feed forward requires solving three major problems:
First, a high order motion profile generator must be designed that can generate smooth changes in position, velocity, acceleration, and jerk. The velocity, acceleration and jerk should be smooth to ensure that the control output generated using the feed forward gains is smooth.
Second, using the derivative gain requires estimating an accurate and smooth velocity. Using the second derivative gain is more challenging because it requires estimating an accurate and smooth acceleration.
Third, how do you tune the jerk feed forward and the second derivative gain? Trial and error is time consuming, so auto tuning must be used.
Two main advantages result from using high order motion target generators. The first is that a physical system cannot possibly follow a linear ramp. This is because following a ramp would require instantaneous changes in acceleration, which, likewise, would require instantaneous changes in force, pressure and flow. The second advantage of using higher-order target generators is that velocity, acceleration, and jerk will vary smoothly from point to point, enabling a smooth control output to be generated.
Estimating velocity and acceleration
The purpose of estimating velocity and acceleration is so that the first and second derivative gains can be used to provide damping for the mass between two springs. The damping allows the actuator to follow the motion profile without overshooting the target velocity and position. The first and second derivatives add electronic damping, which is more efficient than adding friction to increase damping.
Accurately estimating the velocity and acceleration is critical to using the derivative gains. Many people who have tuned PIDs have avoided using the derivative gains because they amplify “noise” and make the control output look noisy.
The simple way of calculating velocity requires knowing the position at two different times and dividing distance by time. This works well if the positions and times are precisely known. Calculating the acceleration usually is done by measuring the speed at two different times, calculating the difference between the two speeds, and dividing the difference by the time.
This seems easy enough, but in practice, it is difficult — in part, due to sensors and loop times. For instance, if the feedback device provides only 0.001 in. resolution and the sample times are at one msec intervals, the resolution of the speed calculation is only 1 in./sec. This is a shortcoming because ramping up or down the target velocity will smoothly ramp through speeds that are not even multiples of 1 in./sec. The measured speed will not match the actual speed most of the time, so the measured speed will be too fast or too slow. And when this error is multiplied by the derivative gain, the error will make the control output look noisy. In reality, the error is not noise but quantizing error — the rounding error caused by variation in the number and values of samples taken in the sampling period.
Calculating the acceleration is even more error prone because if the velocity’s resolution is only 1 in./sec, then over a 1 msec time period the acceleration will have a resolution of 1000 in./sec2, which is not usable at all. In practice, most hydraulic systems usually ramp up and down a rates closer to 100 in./sec2. Clearly, a better way must be found to estimate the velocity and acceleration to make them usable for calculating feed forwards.
A sensible solution
The answer to this problem is to use a model to estimate the velocity and acceleration as a function of the control output. The model is simply a set of equations that use floating point numbers having practically infinite resolution compared to a real feedback device. This eliminates the quantizing error, but the model had better be fairly accurate. To keep the model from going astray, the measured feedback is used to correct the model. Now, the derivative gain can be multiplied by the error between the target and estimated velocity. Similarly, the second derivative gain can be multiplied by the error between the target and the estimated acceleration. Doing so will make the output smoother.
Part Two
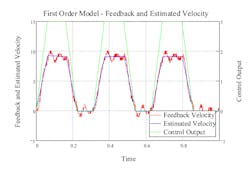
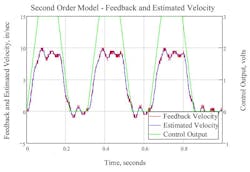
Figures 1 and 2 contain two graphs showing how one can use the measured velocity and the control output to generate a first and second order model respectively. The measured or feedback velocity in red is calculated using a simple method. The resolution of the feedback device is 0.001 inches but the velocity is calculated over a time span of two milliseconds, so the resolution of the feedback velocity is 0.5 inches per second. One can see that the estimated velocity is much smoother because it is generated by the model, but the feedback velocity from a first-order model doesn’t follow the changes in the actual model that well. On the other hand, the estimated velocity for the second order model follows the feedback velocity much more closely than the first order model, and best represents how the actual system is moving. This indicates that the system is a second order system, behaving like a mass between two springs.
So where does the model that is used to estimate the velocity and acceleration come from?
Auto Tuning
Auto tuning is a feature that is supported by some electronic motion control systems and is necessary when using advanced features such as the second derivative gain and the jerk feed forward because few hydraulic control system designers have any experience at tuning them manually. The two parameters can be determined roughly by trial and error but having a method of determining the gain, damping factor and natural frequency quickly is important to reduce startup time and shorten the time it may take to retune a system as the mechanics change.
Auto Tuning
VCCM Equation:
Where:
Fl is the load force that must be overcome,
PS is supply pressure,
APE is the cylinder size,
v is the speed of cylinder propulsion,
KVPL is the degree to which the
valve is open,
ρvis the symmetry of the valve, and
ρcis the cylinder area ratio (cap side of piston area/rod side area).
Natural Frequency:
Where:
β is the bulk modulus of oil,
A is the surface area of the piston,
V is the volume of the cylinder, and
m is the mass of the load
Auto tuning is a way of estimating the model of the actuator and load using the control output to the actuator and the position and velocity response as in the two graphs above. Models can be very complex but usually one can achieve 95% of the benefit with 5% of the effort if the model is kept relatively simple. A hydraulic actuator and load can be modeled simply as a mass between two springs so the model consists of a gain, damping factor and natural frequency. It is possible to estimate the gain and natural frequency at design time using the VCCM equation (See sidebar) and the formula for natural frequency (See sidebar). The damping factor is a little more difficult to estimate, but a typical damping factor is in the range of 0.3 to 0.4. Even a rough estimate of the damping factor can allow the person doing the motion control to enter these parameters into the motion controller’s built-in simulator so that he or she can get started before the machinery is built. Once in the field the controls person can do an auto tune to find the actual gain, damping factor and natural frequency.
Auto tuning isn’t totally automatic. There is a procedure where the actuator must be moved in a specific way, usually via open loop control. The relationship between the control output and the position or velocity data is estimated by trying a value for each of the three parameters (gain, damping factor and natural frequency) and then checking to see how closely the estimated position or velocity follows actual recorded position or velocity. An evaluation can be done by summing the square of all the errors between the estimated and actual position or velocity. The three parameters mentioned above are changed in an effort to minimize the sum of the squared errors. This is a trial and error process but a computer can do it very quickly so it seems instantaneous. When the computer is done it has found the best values of the gain, damping factor and natural frequency.
The Results
A true test is to move the actuator using a sine wave motion profile. The actual or true velocity and acceleration will smoothly go through a range of values and the goal is to estimate the velocity and acceleration accurately so the actuator can follow the target accurately. Low resolution feedback will make the quantizing effect obvious because the velocity calculated directly from the feedback will change in steps. The goal of the model based control is to estimate smooth velocities as shown below.
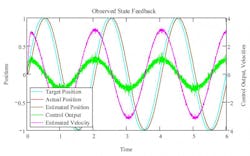
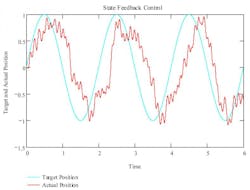
The graph in Figure 3 shows how an actuator with a gain of 3 inches per second, damping factor of 0.4 and a natural frequency of 10 Hz can be controlled using a PID with a second derivative gain. The feedback is truncated to 0.001 inches to simulate a start-stop linear magnetostrictive displacement transducer (LMDT) rod with a position feedback of 0.001 inches. As noted above, the resolution of the measured velocity would be 1 inch per second and the resolution of the acceleration would be 1000 inches per second squared. The graph shows that the estimated position is so close to the actual position that they look like one line. The estimated velocity is relatively smooth compared to what could be achieved doing simple velocity calculations where the resolution would be one inch per second. The control output is basically doing a 1 volt peak to peak sine wave to control the actuator. There is a little noise on the control output due to the errors in estimating the velocity and acceleration but it isn’t bad compared to what would happen without estimating the velocity and acceleration with the model.
If the model wasn’t used the control output would simply be changing from +10 to -10 volt because of the inability to estimate the velocity and acceleration. Without the model based velocity and accelerations, the PID and second derivative gains would need to be drastically reduced in order to keep the control output from swinging 10 volts peak to peak.
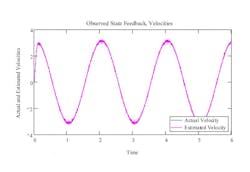
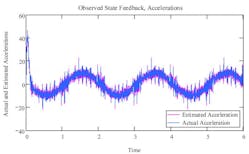
Figure 4 contains a graph of the actual and estimated velocities. There are actually two lines in the plot, but the estimated velocity is almost identical to the actual velocity, so the estimated velocity line is on top of the actual velocity line. Again, notice that there is no 1 inch per second quantizing.As expected, the estimated acceleration(shown in Figure 5) does shows the effects of feedback quantizing, but spikes of four or five inches per second squared are a lot better than errors of 1000 inches per second squared. The estimated acceleration curve still does a good job of following the actual acceleration.
Just for comparison, compare the model based control above to control without the model (shown in Figure 6). The same gains are used as in Figures 3-5 above. The control output isn’t shown because it changes from -10 to +10 volts due to the affect the quantized velocity and acceleration has on the control output. Since the control output is often saturated, the actuator is being controlled as if the valve is a simple on-off directional control valve.
Conclusion
Implementing model based control with an electrohydraulic motion controller that can run second-order algorithms allows one to control systems that would otherwise be uncontrollable because the derivative gains couldn’t be used or the gain values would need to be keep low so the response will be slow. The alternative is to design systems so that the damping factor and natural frequency are high but this increases the system cost.