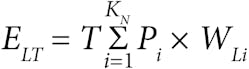Stationary machinery within automated, industrial manufacturing and fabrication processes typically operates in very repetitive, measured, predictable cycles. In these environments, total lost energy over the course of a given time period, say, a day, can be measured or calculated rather easily due to regular, predictable motion cycles.
When it comes to mobile equipment, the cycles are not as regular or predictable, even though they operate “sort of repetitively.” Significant variations occur in each cycle, making lost-power calculation somewhat more challenging.
Vexing variables
Consider the operation of a backhoe excavating a small area, such as a graveyard plot. Variables quickly emerge even in such a confined dig, such as the depth as the project progresses; the reach; and the lift and swing as the dirt piles up. In addition, the operator may not handle the controls in exactly the same manner from cycle to cycle, or the operator may change on another similar project. The number of functions that an operator can manage simultaneously is limited to some degree by the manual dexterity of the operator.
Further variations include soil conditions as the vehicle moves from site to site, and the amount of moisture in the soil, which affects the weight of a bucketful as well as digging resistance. There are doubtless others, but the point is that often widely varying operating conditions make the excavator manufacturer’s job of tuning a machine to “optimal” conditions much more difficult.
The discussion here, though, is hydrostatic transmissions, not excavators. Envisage one used in the drive train of a front-end loader. Its cycle also varies over the course of a day for reasons similar to those already mentioned, as well as others that are particular to front-end loaders. One such example is the amount of travel distance between the load pickup point and the load dump point.
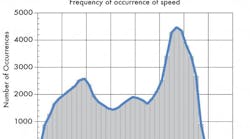
The point is that regular, predictable parts — along with random variations — exist within cyclic operation. Handling these random effects requires statistical methods. For hydrostatic transmission (HSTs), the approach is to use a histogram of the “probability of finding a speed versus the speed” itself, Figure 1.
Generating the histogram
This discussion is not intended to be a treatise on the generalities of statistics or the theory of histograms and their development. Nonetheless, for the statistically challenged reader, it’s helpful to review the steps involved in histogram creation.
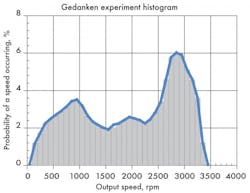
First, it’s important to note that the histograms contained herein are not the result of actual measurements on mobile machinery. Instead, they were developed totally through what the Germans call a gedankenexperiment, that is, by theoretical (mental) estimates. However, the following discussion should explain that the values presented are reasonable for a wheel-driven front-end loader and the histogram creation process as described. The lack of actual histogram data does not in any way affect the procedure or the manner in which conclusions are reached.
To start the explanation, one must interpret the data provided in Figure 1. It consists of a series of 35 bars, each being 100 rpm wide. The vertical axis is simply “Number of occurrences.” A total of 73,980 sampleswent into the chart. The sample counts were put into a series of 100-rpm-wide data buckets; each data bucket is a bar on the graph.
Referring to Figure 1, the height of the bar (a data bucket) with a peak value that’s centered at 2850 rpm, which covers the interval from 2800 to 2900 rpm, represents the number of samples found in that interval. That is, of the 73,980 rpm samples — about 4460 of them — lay between the 2800 and 2900 data bucket. Or, in other words, of the 73,980 speed samples, 4460 of them were in the interval from 2800 to 2900, where the notation 2900 means any tiny amount less than 2900 rpm.
To be useful, the histogram must be converted into one that indicates the “probability of occurring,” expressed as a percentage. This task simply requires dividing each bar amplitude by the total number of samples. In the 2800 to 2900 interval, with its 4460 samples, the result is 4460 ÷ 73,980, about 6.03%.
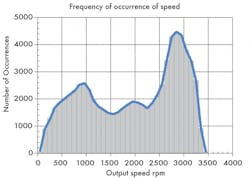
Thus, the modified histogram turns into a probability curve, Figure 2. Therefore, if the machine is operated in a statistically similar manner to that used to generate the histogram data, it will run between 2800 and 2900 rpm about 6% of the time. It will also run, say, between 900 and 1000 rpm about 3.5% of the time.
Collecting histogram data
To collect raw histogram data in a real vehicle in a real working environment, an automated data acquisition system has to be temporarily installed on the vehicle. For the speed histograms of Figures 1 and 2, a speed sensor also must be attached to the output shaft of the HST. Once everything is in place, the data-acquisition system then will read and log the speed data over a predetermined amount of time.
This method, called a sampling process, takes speed samples at precisely regular intervals (samples are also called observationsin data-acquisition jargon). The regular interval may be one second. The exact sampling time interval isn’t important at this time. However, suffice to say, more samples are better than fewer.
At each second of the machine’s operation, the speed is sampled and stored in the data-acquisition/computer memory for later retrieval. During this stage, a statistician can help with the selection of a proper sample interval, the correct number of data buckets, and the total time of sampling. Details regarding those processes are beyond the scope of this brief analytical study.
The example vehicle data (which are not real statistical data) had 73,980 samples. If a 1-sec sampling interval was used, this would cover an operating period of just under 21 hr, which is usually expected in three eight-hour work shifts.
Provided that future vehicle operation resembles its operation during the 21-hr sampling period, expectations are that a new histogram would be similar to that during the sampling period. In other words, the transmission output shaft speed should be between, for example, 2800 and 2900 rpm about 6% of the time, Figure 2.
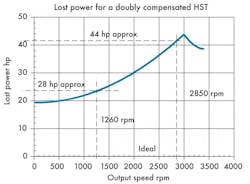
You could go a step further and combine this data with a Power Lost curve, Figure 3. It can be seen that the transmission power loss is almost 44 hp at the interval midpoint of 2850 rpm.
Continuing, consider the interval centered at 1250 rpm. Lost power is about 28 hp; Figure 2 indicates that the machine operates within that speed interval about 2.4% of the time. It should be obvious that lost energy depends not only on the lost power characteristics, but also the amount of time that the machine spends at any chosen operating condition.
The next step is to establish a total time interval for determining the amount of energy that goes into lost power. Perhaps the task is to determine the total energy lost in a typical 8-hr shift, and the machine is in actual operation for 7.5 hr. The total energy lost while operating between 2800 and 2900 rpm is simply the product of the histogram amplitude in that interval (about 6%) times the power lost when operating at that speed (roughly 42 hp) times the total time of operation (7.5 hr). The result is approximately18.9 hp-hr.
Now let’s look at the speed interval centered on 1250 rpm, Figure 3. The lost power in that interval is about 28 hp. Referring to the histogram of Figure 2, the transmission spends about 2.4% of the time at speeds between 1200 and 1300 rpm, so the total energy lost while operating in that speed range over the 7.5 hr is:
7.5 hr ×0.024 ×28 hp = 5.04 hp-hr
The energy lost while operating in the 1250-rpm interval and the 2850-rpm interval is the sum of the two — about 24.84 hp-hr. So, total lost energy is simply the sum of:
(time) ×(probability) ×(lost power)
Summing up the summing up
It should be apparent that calculating the total power lost during the 7.5-hr operating period merely involves multiplying the probability of a speed occurring at each of the 35 histogram intervals, times the power that’s lost at the center point of that interval, times the total operational time of interest. Then all 35 values are added together.
It’s important to note that all of the bar amplitude percentages in the probability histogram, when added together, will equal 100%. This is a requirement of such a histogram. At this point, it’s safe to assume that the probability of finding a speed between 0 and 3500 rpm is 100% for the hydrostatic transmission used in this study. The formula for determining the total energy lost during an arbitrary period of time is:
where:
T= the total time interval for evaluating the lost energy (units of time are arbitrary)
Pi= the probability of a speed occurring in the ith probability histogram interval (numeric)
WLi= the power lost when operating at the midpoint speed of the ith probability histogram interval (hp)
KN= the total number of speed intervals in the probability histogram (numeric)
ELT= the total energy lost during the time interval of T(units depend on those used for T)
Overall, the process is relatively simple if there’s a realistic and typical histogram, and the starting point is the power loss diagram for the transmission. It yields information that relates directly to fuel costs and, ultimately, money down the drain. Such information is not available from the efficiency data.
Part two of this article delves deeper into histogram statistical analysis, concentrating on the low-speed, high-torque region of transmission operation.